Les intérêts composés : L'effet boule de neige de vos finances

Les intérêts composés sont souvent qualifiés de "huitième merveille du monde", une citation généralement attribuée à Albert Einstein qui aurait déclaré :

"Les intérêts composés sont la huitième merveille du monde. Celui qui les comprend, les gagne ; celui qui ne les comprend pas, les paie."

Cette puissante notion est au cœur de la croissance de vos investissements et peut vous aider à atteindre vos objectifs financiers bien plus rapidement que vous ne l’imaginez. Mais comment fonctionnent-ils exactement ? Pour mieux comprendre, imaginons une boule de neige dévalant une colline.

1. L'effet boule de neige

Imaginez que vous commencez avec une petite boule de neige au sommet d'une colline. À mesure qu’elle descend, elle accumule plus de neige et devient de plus en plus grande, même si vous ne faites plus rien pour la pousser. C’est exactement ce qui se passe avec vos intérêts composés. Ils fonctionnent sur le même principe : l’argent que vous investissez aujourd'hui grandit non seulement grâce aux intérêts, mais les nouveaux intérêts générés par votre argent grandissent également avec le temps.

Lorsque vous laissez vos intérêts s’accumuler sur plusieurs périodes, votre argent ne se contente pas de croître, il croît exponentiellement.

Comment ça marche ?

Les intérêts composés se produisent lorsque les intérêts que vous gagnez sur votre épargne ou investissement sont réinvestis, générant ainsi de nouveaux intérêts à leur tour. Voici la formule mathématique pour calculer les intérêts composés :

Valeur future = Capital initial × (1 + taux d'intérêt)^nombre de périodes

• Valeur future : la somme que vous aurez après une certaine période.
• Capital initial : le montant de départ que vous investissez.
• Taux d'intérêt : le taux auquel vos investissements croissent.
• Nombre de périodes : le nombre de fois où les intérêts sont calculés et ajoutés à votre capital.

Exemple :

Prenons un exemple simple. Si vous investissez 1000 € avec un taux d'intérêt de 5 % et que les intérêts sont composés chaque année, voici ce qui se passe après 5 ans.

Valeur future = 1000 × (1 + 0,05)^5 = 1000 × 1,276 = 1276,3 €

Cela signifie qu'au bout de 5 ans, votre investissement aura grandi à 1276,3 €. Mais voici la beauté des intérêts composés : plus vous laissez cet argent fructifier longtemps, plus il grandira rapidement.

2. L’importance du temps

Les intérêts composés nécessitent du temps pour atteindre leur plein potentiel, un peu comme planter un arbre. Imaginez planter un gland aujourd’hui. Il ne devient pas un chêne du jour au lendemain. Mais, au fil des années, ce gland grandit, se transforme en un jeune arbre, puis en un magnifique chêne. L’arbre grandit d’autant plus qu’il a eu le temps de pousser.

De la même manière, plus vous commencez à épargner tôt, plus vous laissez du temps à vos intérêts composés pour "pousser" et générer de la richesse. Plus vous attendez, plus vous retardez la croissance exponentielle de vos économies.

Conseil : Commencez à investir dès que possible, même avec de petites sommes. Vous serez surpris de voir à quel point la magie des intérêts composés fonctionne au fil du temps.

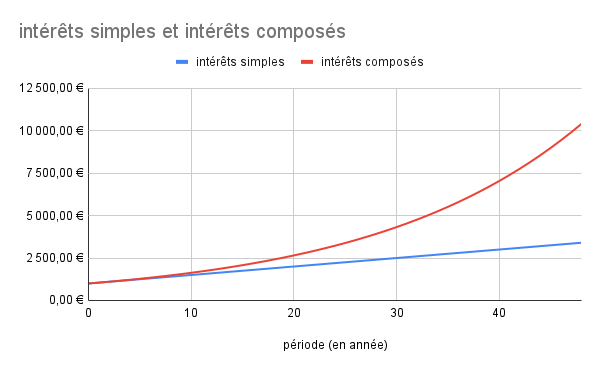
3. Les intérêts composés vs les intérêts simples

Pour comprendre encore mieux la puissance des intérêts composés, comparons-les aux intérêts simples.

• Intérêts simples : Dans le cas des intérêts simples, vous ne gagnez des intérêts que sur votre capital de départ, sans jamais réinvestir les intérêts. Par exemple, si vous investissez 1000 € à 5 % d’intérêts simples pendant 5 ans, vous gagnerez 50 € par an, soit un total de 250 € après 5 ans. Le montant total sera de 1250 €.

• Intérêts composés : Non seulement vous gagnez des intérêts sur votre capital de départ, mais les intérêts générés sont eux-mêmes réinvestis et produisent de nouveaux intérêts. Avec un taux de 5 % d’intérêts composés, vous ne gagnez pas seulement 50 € la première année, mais aussi des intérêts sur les 50 € supplémentaires au fil des ans. Résultat : vous obtenez 1276,3 € après 5 ans, comme nous l'avons vu plus haut.

La différence peut sembler petite au départ, mais elle devient significative au fil des années. En effet continuons notre comparaison sur un période plus longue disons 20 ans.

Comparaison sur 20 ans

• Intérêts simples : Gardons notre exemple avec un investissement de départ de 1000 € et un taux d’intérêt de 5 %. Chaque année, vous gagnez 5 % de 1000 €, soit 50 €. Après 20 ans, vous aurez gagné 50 € × 20 = 1000 € en intérêts simples.

Le montant total après 20 ans serait donc :

1000 € (capital initial) + 1000 € (intérêts) = 2000 €

• Intérêts composés : Passons maintenant aux intérêts composés et utilisons la même somme de départ de 1000 € avec un taux d’intérêt de 5 %, composés annuellement, sur 20 ans.

Appliquons la formule pour calculer la valeur après 20 ans avec les intérêts composés :

Valeur future = 1000 € × (1 + 0,05)^20 = 1000 € × 2,653 = 2653 €

Voici la différence entre les deux types d’intérêts après 20 ans :

• Intérêts simples : Vous avez 2000 € (1000 € de capital + 1000 € d'intérêts).
• Intérêts composés : Vous avez 2653 € (1000 € de capital + 1653 € d'intérêts).

La différence est 653 € de plus avec les intérêts composés !

Un écart qui se creuse avec le temps

Plus vous laissez vos intérêts se composer sur une longue période, plus l’écart entre les intérêts simples et composés se creuse. Avec les intérêts simples, vous gagnez un montant fixe chaque année. Avec les intérêts composés, vos gains augmentent exponentiellement à chaque période, car les intérêts eux-mêmes génèrent des intérêts.

Voyons ce qui se passe après 30 ans pour le même exemple :

• Intérêts simples : Vous aurez gagné 50 € × 30 = 1500 €, soit un total de 2500 €.
• Intérêts composés : Calculons la valeur future après 30 ans avec la même formule :

Valeur future = 1000 € × (1 + 0,05)^30 = 1000 € × 4,322 = 4322 €

Après 30 ans, vous aurez 4322 € avec les intérêts composés, contre 2500 € avec les intérêts simples. L’écart est maintenant de 1822 €.

C’est cette différence exponentielle qui fait toute la puissance des intérêts composés sur le long terme.

Comme le montre cet exemple, les intérêts composés offrent des gains exponentiels qui ne cessent de croître avec le temps, bien au-delà de ce que vous pourriez obtenir avec des intérêts simples. Plus vous laissez vos investissements fructifier longtemps, plus vous constaterez à quel point cette stratégie est puissante pour créer de la richesse sur le long terme.

4. Comment maximiser l’effet des intérêts composés ?

Voici quelques conseils pour tirer pleinement parti de cette stratégie financière :

a. Investir tôt

Comme mentionné précédemment, le facteur temps est primordial. Plus vous commencez tôt, plus les intérêts composés auront de temps pour faire des merveilles.

b. Réinvestir les intérêts

Si vous retirez vos intérêts, vous cassez la boucle des intérêts composés. Assurez-vous de réinvestir les intérêts générés pour qu'ils continuent à travailler pour vous.

c. Choisir des placements avec des taux d'intérêt attractifs

Le taux d'intérêt joue un rôle majeur. Un taux plus élevé signifie une croissance plus rapide. Cherchez des placements avec des rendements raisonnables et durables pour maximiser vos gains.

Conclusion

Les intérêts composés sont comme un moteur caché dans vos finances, travaillant sans relâche en arrière-plan pour faire croître votre argent, à condition de lui laisser du temps et de ne pas interrompre le processus. Tout comme une boule de neige devient une avalanche ou un gland devient un chêne, vos économies peuvent croître de manière exponentielle avec les intérêts composés.

Alors, pourquoi ne pas commencer à cultiver votre patrimoine dès aujourd’hui ? Investissez dans des placements à long terme, réinvestissez vos gains, et laissez les intérêts composés vous conduire vers la liberté financière.